Diclib.com
Wörterbuch ChatGPT

Wörterbuchsuche Kundenspezifische Lösungen

Geben Sie ein Wort oder eine Phrase in einer beliebigen Sprache ein 👆

Sprache:

Übersetzung und Analyse von Wörtern durch künstliche Intelligenz ChatGPT

Auf dieser Seite erhalten Sie eine detaillierte Analyse eines Wortes oder einer Phrase mithilfe der besten heute verfügbaren Technologie der künstlichen Intelligenz:

wie das Wort verwendet wird
Häufigkeit der Nutzung
es wird häufiger in mündlicher oder schriftlicher Rede verwendet
Wortübersetzungsoptionen
Anwendungsbeispiele (mehrere Phrasen mit Übersetzung)
Etymologie

Was (wer) ist Множеств теория - definition

РАЗДЕЛ МАТЕМАТИКИ

Наивная теория множеств; Теория множеств Кантора; Множеств теория; Дескриптивная теория множеств; История теории множеств; Канторовская теория множеств; Аксиоматическая теория множеств; Аксиоматика теории множеств; Интуитивная теория множеств

$Декартово произведение <math>\{x,y,z\} \times \{1,2,3\}</math>$
$Представление порядковых чисел до <math>\omega^\omega</math>$

МНОЖЕСТВ ТЕОРИЯ

раздел математики, в котором изучаются общие свойства множеств, преимущественно бесконечных. Понятие множества - простейшее математическое понятие, оно не определяется, а лишь поясняется при помощи примеров: множество книг на полке, множество точек на прямой (точечное множество) и т. д. То, что данный предмет (элемент, точка) х принадлежит множеству М, записывают х О М. М. т. лежит в основе многих математических дисциплин; она оказала глубокое влияние на понимание предмета самой математики. Об относящихся сюда понятиях см. Подмножество, Объединение множеств, Пересечение множеств, Пустое множество, Счетное множество, Континуум.

Множеств теория

учение об общих свойствах множеств, преимущественно бесконечных. Понятие множества, или совокупности, принадлежит к числу простейших математических понятий; оно не определяется, но может быть пояснено при помощи примеров. Так, можно говорить о множестве всех книг, составляющих данную библиотеку, множестве всех точек данной линии, множестве всех решений данного уравнения. Книги данной библиотеки, точки данной линии, решения данного уравнения являются элементами соответствующего множества. Чтобы определить множество, достаточно указать характеристическое свойство элементов, т. е. такое свойство, которым обладают все элементы этого множества и только они. Может случиться, что данным свойством не обладает вообще ни один предмет; тогда говорят, что это свойство определяет пустое множество. То, что данный предмет х есть элемент множества М, записывают так: х ∈ М (читают: х принадлежит множеству М).

Подмножества. Если каждый элемент множества А является в то же время элементом множества В, то множество А называется подмножеством, или частью, множества В. Это записывают так: A ⊆ В или В ⊇ А. Т. о., подмножеством данного множества В является и само множество В. Пустое множество, по определению, считают подмножеством всякого множества. Всякое непустое подмножество А данного множества В, отличное от всего множества В, называют правильной частью последнего.

Мощность множеств. Первым вопросом, возникшим в применении к бесконечным множествам, был вопрос о возможности их количественного сравнения между собой. Ответ на этот и близкие вопросы дал в конце 70-х гг. 19 в. Г. Кантор, основавший М. т. как математическую науку. Возможность сравнительной количественной оценки множеств опирается на понятие взаимно однозначного соответствия между двумя множествами. Пусть каждому элементу множества А поставлен в соответствие в силу какого бы то ни было правила или закона некоторый определённый элемент множества В; если при этом каждый элемент множества оказывается поставленным в соответствие одному и только одному элементу множества А, то говорят, что между множествами А и В установлено взаимно однозначное, или одно-однозначное, соответствие [сокращённо: (1-1)-соответствие]. Очевидно, между двумя конечными множествами можно установить (1-1)-соответствие тогда и только тогда, когда оба множества состоят из одного и того же числа элементов. В обобщение этого факта определяют количественную эквивалентность, или равномощность, двух бесконечных множеств как возможность установить между ними (1-1)-соответствие.

Ещё до создания М. т. Б. Больцано владел, с одной стороны, вполне точно формулированным понятием (1-1)-соответствия, а с другой стороны, считал несомненным существование бесконечностей различных ступеней; однако он не только не сделал (1-1)-соответствие основой установления количественной равносильности множеств, но решительно возражал против этого. Больцано останавливало то, что бесконечное множество может находиться в (1-1)-соответствии со своей правильной частью. Например, если каждому натуральному числу n поставить в соответствие натуральное число 2n, то получим (1-1)-соответствие между множеством всех натуральных и множеством всех чётных чисел. Вместо того чтобы в применении к бесконечным множествам отказаться от аксиомы: часть меньше целого, Больцано отказался от взаимной однозначности как критерия равномощности и, т. о., остался вне основной линии развития М. т. В каждом бесконечном множестве М имеется (как легко доказывается) правильная часть, равномощная всему М, тогда как ни в одном конечном множестве такой правильной части найти нельзя. Поэтому наличие правильной части, равномощной целому, можно принять за определение бесконечного множества (Р. Дедекинд).

Для двух бесконечных множеств А и В возможны лишь следующие три случая: либо А есть правильная часть, равномощная В, но в В нет правильной части, равномощной А; либо, наоборот, в В есть правильная часть, равномощная А, а в А нет правильной части, равномощной В; либо, наконец, в А есть правильная часть, равномощная В, и в В есть правильная часть, равномощная А. Доказывается, что в третьем случае множества А и B равномощны (теорема Кантора - Бернштейна). В первом случае говорят, что мощность множества А больше мощности множества В, во втором - что мощность множества В больше мощности множества А. A priori возможный четвёртый случай - в А нет правильной части, равномощной В, а в В нет правильной части, равномощной А, - в действительности не может осуществиться (для бесконечных множеств).

Ценность понятия мощности множества определяется существованием неравномощных бесконечных множеств. Например, множество всех подмножеств данного множества М имеет мощность большую, чем множество М. Множество, равномощное множеству всех натуральных чисел, называется счётным множеством. Мощность счётных множеств есть наименьшая мощность, которую может иметь бесконечное множество; всякое бесконечное множество содержит счётную правильную часть. Кантор доказал, что множество всех рациональных и даже всех алгебраических чисел счётно, тогда как множество всех действительных чисел несчётно. Тем самым было дано новое доказательство существования т. н. трансцендентных чисел, т. е. действительных чисел, не являющихся корнями никакого алгебраического уравнения с целыми коэффициентами (и даже несчётность множества таких чисел). Мощность множества всех действительных чисел называется мощностью континуума. Множеству всех действительных чисел равномощны: множество всех подмножеств счётного множества, множество всех комплексных чисел и, следовательно, множество всех точек плоскости, а также множество всех точек трёх- и вообще n-мерного пространства при любом n. Кантор высказал гипотезу (т. н. континуум-гипотезу): всякое множество, состоящее из действительных чисел, либо конечно, либо счётно, либо равномощно множеству всех действительных чисел; по поводу этой гипотезы и существенных связанных с нею результатов см. Континуума проблема.

Отображения множеств. В М. т. аналитическое понятие функции, геометрическое понятие отображения или преобразования фигуры и т. п. объединяются в общее понятие отображения одного множества в другое. Пусть даны два множества Х и Y, пусть каждому элементу х ∈ Х поставлен в соответствие некоторый определённый элемент у = f(x) множества Y; тогда говорят, что имеется отображение множества Х в множество Y, или что имеется функция, аргумент х которой пробегает множество X, а значения у принадлежат множеству Y; при этом для каждого данного х ∈ Х элемент у = f(x) множества Y называется образом элемента х ∈ Х при данном отображении или значением данной функции для данного значения её аргумента х.

Примеры. 1) Пусть задан в плоскости с данной на ней прямоугольной системой координат квадрат с вершинами (0; 0), (0; 1), (1; 0), (1; 1) и осуществлена проекция этого квадрата, например на ось абсцисс; эта проекция есть отображение множества Х всех точек квадрата на множество Y всех точек его основания; точке с координатами (х; у) соответствует точка (х; 0).

2) Пусть Х - множество всех действительных чисел; если для каждого действительного числа x ∈ X положить у = f(x) = x³, то тем самым будет установлено отображение множества Х в себя.

3) Пусть Х - множество всех действительных чисел; если для каждого х ∈ Х положить у = f(x) = arctg х, то этим будет установлено отображение множества Х на интервал ( - π/2, π/2).

(1-1)-соответствие между двумя множествами Х и Y есть такое отображение множества Х в множество Y, при котором каждый элемент множества Y является образом одного и только одного элемента множества X. Отображения примеров 2) и 3) взаимно однозначны, примера 1) - нет.

Операции над множествами. Суммой, или объединением, двух, трёх, вообще произвольного конечного или бесконечного множества множеств называется множество всех тех предметов, каждый из которых есть элемент хотя бы одного из данных множеств-слагаемых. Пересечением двух, трёх, вообще любого конечного или бесконечного множества множеств называется множество всех элементов, общих всем данным множествам. Пересечение даже двух непустых множеств может быть пустым. Разностью между множеством В и множеством А называется множество всех элементов из В, не являющихся элементами из А: разность между множеством В и его частью А называется дополнением множества А в множестве В.

Операции сложения и пересечения множеств удовлетворяют условиям сочетательности и переместительности (см. Ассоциативность, Коммутативность). Операция пересечения, кроме того, распределительна по отношению к сложению и вычитанию. Эти действия обладают тем общим свойством, что если их производить над множествами, являющимися подмножествами одного и того же множества М, то и результат будет подмножеством множества М. Указанным свойством не обладает т. н. внешнее умножение множеств: внешним произведением множеств Х и Y называется множество Х × У всевозможных пар (х, у), где х ∈ Х, y ∈ Y. Другим в этом смысле "внешним" действием является "возведение в степень": степенью Y^X называется множество всех отображений множества Х в множество Y. Можно определить внешнее умножение любого множества множеств так, что в случае совпадения множителей оно перейдёт в возведение в степень. Если ξ и η мощности множеств Х и Y, то ξη и η^ξ определяются соответственно как мощности множеств Х × Y и Y^Х, что в случае конечных множеств согласуется с умножением и возведением в степень натуральных чисел. Аналогично определяется сумма мощностей как мощность суммы попарно непересекающихся множеств с заданными мощностями.

Упорядоченные множества. Установить в данном множестве Х порядок - значит установить для некоторых пар x', х" элементов этого множества какое-то правило предшествования (следования), выражаемое словами "элемент x' предшествует элементу х", x' < х"", или, что то же, "элемент x' следует за элементом х", x' < х"", причём предполагается выполненным условие транзитивности: если х < x' и x' < х", то х < х". Множество, рассматриваемое вместе с каким-нибудь установленным в нём порядком, называется "частично упорядоченным множеством"; иногда вместо "частично упорядоченное множество" говорят "упорядоченное множество" (Н. Бурбаки). Однако чаще упорядоченным множеством называется такое частично упорядоченное множество, в котором порядок удовлетворяет следующим дополнительным требованиям ("линейного порядка"): 1) никакой элемент не предшествует самому себе; 2) из всяких двух различных элементов х, x' один предшествует другому, т. е. или х < x', или x' < х.

Примеры. 1) Всякое множество

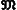
, элементами которого являются некоторые множества х, является "частично упорядоченным ''по включению''": х < x', если х ⊂ x'.

2) Любое множество функций f, определённых на числовой прямой, частично упорядочено, если положить f₁ < f₂, тогда и только тогда, когда для каждого действительного числа х имеем f₁(x) ≤ f₂(x).

3) Всякое множество действительных чисел линейно упорядочено: меньшее из двух чисел считается предшествующим большему.

Два упорядоченных множества называются подобными между собой, или имеющими один и тот же порядковый тип, если между ними можно установить (1-1)-соответствие, сохраняющее порядок. Элемент упорядоченного множества называется первым, если он предшествует в этом упорядоченном множестве всем остальным элементам; аналогично определяется и последний элемент. Примеры: в упорядоченном множестве всех действительных чисел нет ни первого, ни последнего элемента; в упорядоченном множестве всех неотрицательных чисел нуль есть первый элемент, а последнего элемента нет; в упорядоченном множестве всех действительных чисел x, удовлетворяющих неравенствам а ≤ х ≤ b, число а есть первый элемент, b - последний.

Упорядоченное множество называется вполне упорядоченным, если оно само и всякое его правильное подмножество имеют первый элемент. Порядковые типы вполне упорядоченных множеств называются порядковыми, или ординальными, числами. Если вполне упорядоченное множество конечно, то его порядковое число есть обычное порядковое число элементарной арифметики. Порядковые типы бесконечных вполне упорядоченных множеств называются трансфинитными числами (См. Трансфинитные числа).

Точечные множества. Теория точечных множеств, т. е. в первоначальном понимании слова - теория множеств, элементами которых являются действительные числа (точки числовой прямой), а также точки двух-, трёх- и вообще n-мерного пространства, основана Г. Кантором, установившим понятие предельной точки (См. Предельная точка) множества и примыкающие к нему понятия замкнутого множества (См. Замкнутые множества) и др. Дальнейшее развитие теории точечных множеств привело к понятиям метрического пространства (См. Метрическое пространство) и топологического пространства (См. Топологическое пространство), изучением которых занимается общая Топология. Наиболее самостоятельное существование ведёт дескриптивная теория множеств. Основанная французскими математиками Р. Бэром и А. Лебегом в связи с классификацией разрывных функций (1905), дескриптивная М. т. началась с изучения и классификации т. н. борелевских множеств (B-множеств). Борелевские множества определяются как множества, могущие быть построенными, отправляясь от замкнутых множеств, применением операций сложения и пересечения в любых комбинациях, но каждый раз к конечному или к счётному множеству множеств. А. Лебег показал, что те же множества - и только они - могут быть получены как множества точек, в которых входящая в Бэра классификацию (См. Бэра классификация) действительная функция f(x) обращается в нуль или, более общо, удовлетворяет условию вида а < f(x) ≤ b. Дальнейшее развитие дескриптивной М. т. было осуществлено преимущественно русскими и польскими математиками, особенно московской школой, созданной Н. Н. Лузиным (П. С. Александров, М. Я. Суслин, М. А. Лаврентьев, А. Н. Колмогоров, П. С. Новиков). Александров доказал теорему (1916) о том, что всякое несчётное борелевское множество имеет мощность континуума. Аппарат этого доказательства был применен Суслиным для построения теории А-множеств, охватывающих как частный случай борелевские (или В-) множества (считавшиеся до того единственными множествами, принципиально могущими встретиться в анализе). Суслин показал, что множество, дополнительное к А-множеству М, является само А-множеством только в том случае, когда множество М - борелевское (дополнение к борелевскому множеству есть всегда борелевское множество). При этом А-множества оказались совпадающими с непрерывными образами множества всех иррациональных чисел. Теория А-множеств в течение нескольких лет оставалась в центре дескриптивной М. т. до того, как Лузин пришёл к общему определению проективных множеств, которые могут быть получены, отправляясь от множества всех иррациональных чисел при помощи повторного применения операции вычитания и непрерывного отображения. К теории А-множеств и проективных множеств относятся также работы Новикова и др. Дескриптивная М. т. тесно связана с исследованиями по основаниям математики (с вопросами эффективной определимости математических объектов и разрешимости математических проблем).

Значение М. т. Влияние М. т. на развитие современной математики очень велико. Прежде всего, М. т. явилась фундаментом ряда новых математических дисциплин (теории функций действительного переменного, общей топологии, общей алгебры, функционального анализа и др.).

Постепенно теоретико-множественные методы находят всё большее применение и в классических частях математики. Например, в области математического анализа они широко применяются в качественной теории дифференциальных уравнений, вариационном исчислении, теории вероятностей и др.

Наконец, М. т. оказала глубокое влияние на понимание самого предмета математики (См. Математика) или таких её больших отделов, как Геометрия. Только М. т. позволила отчётливо сформулировать понятие Изоморфизма систем объектов, заданных вместе со связывающими их отношениями, и привела к пониманию того обстоятельства, что каждая математическая теория в её чистой абстрактной форме изучает ту или иную систему объектов лишь "с точностью до изоморфизма", т. е. может быть без всяких изменений перенесена на любую систему объектов, изоморфную той, для изучения которой теория была первоначально создана.

Что касается М. т. в вопросах обоснования математики, т. е. создания строгого, логически безупречного построения математических теорий, то следует иметь в виду, что сама М. т. нуждается в обосновании применяемых в ней методов рассуждения. Более того, все логические трудности, связанные с обоснованием математического учения о бесконечности (см. Бесконечность в математике), при переходе на точку зрения общей М. т. приобретают лишь большую остроту (см. Аксиоматическая теория множеств, Логика, Конструктивная математика, Континуум).

Лит.: Лузин Н. Н., Теория функций действительного переменного, 2 изд., М., 1948; Александров П. С., Введение в общую теорию множеств и функций, М. - Л., 1948; Хаусдорф Ф., Теория множеств, пер. с нем., М. - Л., 1937.

П. С. Александров.

МНОЖЕСТВ ТЕОРИЯ

Под множеством понимается совокупность каких-либо объектов, называемых элементами множества. Теория множеств занимается изучением свойств как произвольных множеств, так и множеств специального вида независимо от природы образующих их элементов. Терминология и многие результаты этой теории широко используются в математике, например в математическом анализе, геометрии и теории вероятностей.

Терминология. Если каждый элемент множества B является элементом множества A, то множество B называется подмножеством множества A. Например, если множество A состоит из чисел 1, 2 и 3, то у него существует 8 подмножеств (три из них содержат по 1 элементу, три - содержат по 2 элемента, одно подмножество, по определению, есть само множество A и восьмое подмножество - это пустое множество, не содержащее ни одного элемента). Запись x . A означает, что x - элемент множества A, а B . A - что B является подмножеством множества A. Если универсальное множество, из которого мы берем элементы всех множеств, обозначить через I, то элементы, принадлежащие I, но не входящие в A, образуют множество, называемое дополнением множества A и обозначаемое C(A) или A?. Множество, не содержащее ни одного элемента, называется пустым множеством.

Над множествами можно производить операции, напоминающие операции, производимые в арифметике над числами. Объединением AB множеств A и B называется множество, состоящее из всех элементов, принадлежащих хотя бы одному из множеств A и B (элемент, принадлежащий множествам A и B одновременно засчитывается при включении в AB только один раз). Пересечением AB множеств A и B называется множество, состоящее из всех элементов, принадлежащих как A, так и B. Предположим, например, что множество I состоит из всех букв русского алфавита, A - из всех согласных, а множество B - из букв, встречающихся в слове "энциклопедия". Тогда объединение AB состоит из всех букв алфавита, кроме а, ё, у, ъ, ь, ы, ю, пересечение AB - из букв д, к, л, н, п, ц, а дополнение C(A) - из всех гласных. Раздел теории множеств, который занимается исследованием операций над множествами, называется алгеброй множеств. Пустое множество играет в алгебре множеств роль нуля, и поэтому его часто обозначают символом О; например, AO = A, AO = O.

Булева алгебра. Алгебра множеств является подразделом булевых алгебр, впервые возникших в трудах Дж.Буля (1815-1864). В аксиомах булевой алгебры отражена аналогия между понятиями "множества", "событие" и "высказывания". Логические высказывания можно записать с помощью множеств и проанализировать с помощью булевой алгебры.

Даже не вдаваясь в детальное изучение законов булевой алгебры, мы можем получить представление о том, как она используется на примере одной из логических задач Льюиса Кэрролла. Пусть у нас имеется некоторый набор утверждений:

1. Не бывает котенка, который любит рыбу и которого нельзя научить всяким забавным штукам;

2. Не бывает котенка без хвоста, который будет играть с гориллой;

3. Котята с усами всегда любят рыбу;

4. Не бывает котенка с зелеными глазами, которого можно научить забавным штукам;

5. Не бывает котят с хвостами, но без усов.

Какое заключение можно вывести из этих утверждений?

Рассмотрим следующие множества (универсальное множество I включает в себя всех котят): A - котята, любящие рыбу; B - котята, обучаемые забавным штукам; D - котята с хвостами; E - котята, которые будут играть с гориллой; F - котята с зелеными глазами и G - котята с усами. Первое утверждение гласит, что множество котят, которые любят рыбу, и дополнение множества котят, обучаемых забавным штукам, не имеют общих элементов. Символически это записывается как

1. AC(B) = O.

Аналогичным образом остальные утверждения можно записать так:

2. C(D)E = O;

3. G . A;

4. BF = O;

5. D . G.

Принимая во внимание теоретико-множественный смысл символов (или воспользовавшись законами булевой алгебры), мы можем переписать утверждения 1, 2 и 4 в виде

1. A . B;

2. E . D;

4. B . C(F).

Таким образом, мы переформулировали исходные утверждения в следующие:

1. Котят, которые любят рыбу, можно обучить забавным штукам;

2. У котят, которые будут играть с гориллой, есть хвосты;

4. У котят, которых можно обучить забавным штукам, глаза не зеленые;

Теперь можно расположить символические записи утверждений в таком порядке, чтобы последний символ предыдущего утверждения совпадал с первым символом следующего (этому условию удовлетворяет расположение утверждений в порядке 2, 5, 3, 1, 4). Возникает цепочка включений E . D . G . A . B . C(F), из которой можно сделать вывод, что E . C(F) или "Не бывает котенка с зелеными глазами, который будет играть с гориллой". Такое заключение едва ли очевидно, если рассматривать пять исходных утверждений в их словесной формулировке.

Сравнение множеств. Если из элементов двух множеств можно составить пары таким образом, чтобы каждому элементу первого множества соответствовал определенный элемент второго множества, а каждому элементу второго множества соответствовал один и только один элемент первого множества, то говорят, что между такими двумя множествами установлено взаимно однозначное соответствие. Чтобы установить взаимно однозначное соответствие, необязательно пересчитывать элементы множеств. Например, мы знаем, что американские штаты находятся во взаимно однозначном соответствии с их столицами, хотя можем оставаться в неведении относительно общего их числа. Мы могли бы утверждать: "Столиц штатов ровно столько, сколько штатов". Между двумя конечными множествами можно установить взаимно однозначное соответствие тогда и только тогда, когда оба множества состоят из одного и того же числа элементов. В теории множеств аналогичные утверждения используются, даже когда множества содержат бесконечно много элементов. Если между двумя множествами можно установить взаимно однозначное соответствие, то говорят, что они имеют одинаковое количество элементов или равномощны. Если же при любом способе образования пар некоторые элементы из первого множества остаются без пары, то говорят, что первое множество содержит больше элементов, чем второе, или, что первое множество имеет большую мощность. С понятием мощности связаны, казалось бы, удивительные результаты. Например, на первый взгляд положительных целых чисел в два раза больше, чем четных положительных чисел, так как четно каждое второе число. Но, согласно теории множеств, четных положительных чисел столько же, сколько всех положительных целых чисел. Действительно, можно образовать пары чисел 2 и 1, 4 и 2, 6 и 3 и, вообще каждому четному числу 2n поставить в соответствие целое число n. Именно это обстоятельство имел в виду Б.Рассел (1872-1970), сформулировав факт, названный им парадоксом Тристрама Шенди. Герой романа Стерна сетовал на то, что ему потребовался целый год, чтобы изложить события первого дня его жизни, еще один год понадобился, чтобы описать второй день, и что при таком темпе он никогда не завершит свое жизнеописание. Рассел возразил, заметив, что если бы Тристрам Шенди жил вечно, то смог бы закончить свое жизнеописание, так как события n-го дня Шенди мог бы описать за n-й год и, таким образом, в летописи его жизни ни один день не остался бы не запечатленным. Иначе говоря, если бы жизнь длилась бесконечно, то она насчитывала бы столько же лет, сколько дней. Эти примеры показывают, что бесконечное множество можно поставить во взаимно однозначное соответствие со своим бесконечным подмножеством. Иногда это свойство принимают за определение бесконечного.

Если можно установить взаимно однозначное соответствие между некоторым множеством и множеством положительных целых чисел, то говорят, что такое множество счетно. Для обозначения количества элементов в счетном множестве часто используют символ ?0 (алеф-нуль). Так называемые "трансфинитные" числа, например ?0, могут не подчиняться обычным законам арифметики. Например, так как существует ?0 четных чисел, ?0 нечетных и ?0 целых чисел, то приходится признать, что ?0 + ?0 = ?0. Идея сравнения множеств путем установления взаимно однозначного соответствия между ними используется в различных разделах математики. Число всех действительных чисел, как показал основатель научной теории множеств Г.Кантор (1845-1918), больше, чем ?0 чисел. Следовательно, если можно показать, что множество действительных чисел, обладающих некоторым особым свойством, является всего лишь счетным множеством, то заведомо должны существовать действительные числа, этим свойством не обладающие. Например, так как множество алгебраических чисел счетно, должны существовать неалгебраические числа. Такие числа называются трансцендентными.

Поразительная и далеко не очевидная теорема, высказанная в качестве гипотезы Кантором и доказанная Э.Шрёдером и Ф.Бернштейном около 1896, утверждает, что если можно установить взаимно однозначное соответствие между множеством A и подмножеством множества B, и между множеством B и подмножеством множества A, то существует взаимно однозначное соответствие между всем множеством A и всем множеством B.

Парадоксы. Мы уже упоминали о том, что в теории множеств встречаются такие утверждения, как парадокс Тристрама Шенди, которые выглядят противоречащими здравому смыслу. Эти парадоксы возникают просто потому, что теория множеств, подобно многим математическим и физическим теориям, облекает свои идеи в обычные слова, вкладывая в них особый смысл. Однако существуют и парадоксы, возникающие из-за внутренних логических трудностей самой теории множеств. Обильным источником парадоксов такого типа служит широко распространенная практика задания множества путем указания некоторого свойства его элементов, например, "множество, состоящее из английских слов, содержащих менее 19 букв".

Некритическое использование такого рода определений может привести к трудностям. Например, некоторые статьи в этой энциклопедии содержат ссылки на себя, другие таких ссылок не содержат. Мы могли бы включить в нашу энциклопедию дополнительную статью, состоящую только из перечня статей, не содержащих ссылок на себя. Принадлежала бы такая статья множеству статей, не содержащих ссылок на себя, или не принадлежала бы. Любой ответ противоречил бы отличительному свойству, которым по их определению наделены элементы множества. Это - одна из форм так называемого парадокса Рассела, названного в честь своего автора Бертрана Рассела. "Множество всех множеств" - еще одно понятие, также приводящее к парадоксу. Существование парадоксов показывает, с какой осторожностью следует пользоваться терминологией теории множеств. Тем не менее теория множеств настолько полезна, что большинство математиков не хотели бы отказываться от нее. Было затрачено много усилий, чтобы развить методы, позволяющие исключить возникновение парадоксов в теории множеств. В приложениях теории множеств к другим разделам математики универсальное множество I обычно само является некоторым определенным множеством и парадоксальные ситуации здесь не возникают.

Аксиома выбора. Неожиданные трудности в теории множеств могут возникнуть, казалось бы, в самых простых случаях. Если, например, задано семейство непересекающихся множеств, ни одно из которых не пусто, то интуитивно кажется очевидным, что мы можем построить новое множество, содержащее ровно по одному элементу из каждого множества, входящего в это семейство. Но если наше семейство содержит бесконечно много множеств, то для построения нового множества может потребоваться бесконечное число произвольных выборов, а законность такого процесса при тщательном анализе становится отнюдь не очевидной. Аксиома выбора, утверждающая, что такое множество существует, была впервые сформулирована в 1904 Э.Цермело (1871-1953). До сих пор не удалось показать, что аксиома выбора следует из остальных аксиом теории множеств. Но около 1938 К.Гёдель (1906-1978) показал, что если теория множеств непротиворечива (т.е. не содержит внутренних противоречий) без аксиомы выбора, то она остается непротиворечивой и после присоединения к ней аксиомы выбора. См. также АБСТРАКТНЫЕ ПРОСТРАНСТВА; ФУНКЦИЯ.

Wikipedia

Теория множеств

Тео́рия мно́жеств — раздел математики, в котором изучаются общие свойства множеств — совокупностей элементов произвольной природы, обладающих каким-либо общим свойством. Создана во второй половине XIX века Георгом Кантором при значительном участии Рихарда Дедекинда, привнесла в математику новое понимание природы бесконечности, была обнаружена глубокая связь теории с формальной логикой, однако уже в конце XIX — начале XX века теория столкнулась со значительными сложностями в виде возникающих парадоксов, поэтому изначальная форма теории известна как наивная теория множеств. В XX веке теория получила существенное методологическое развитие, были созданы несколько вариантов аксиоматической теории множеств, обеспечивающие универсальный математический инструментарий, в связи с вопросами измеримости множеств тщательно разработана дескриптивная теория множеств.

Теория множеств стала основой многих разделов математики — общей топологии, общей алгебры, функционального анализа и оказала существенное влияние на современное понимание предмета математики. В первой половине XX века теоретико-множественный подход был привнесён и во многие традиционные разделы математики, в связи с чем стал широко использоваться в преподавании математики, в том числе в школах. Однако использование теории множеств для логически безупречного построения математических теорий осложняется тем, что она сама нуждается в обосновании своих методов рассуждения. Более того, все логические трудности, связанные с обоснованием математического учения о бесконечности, при переходе на точку зрения общей теории множеств приобретают лишь бо́льшую остроту.

Начиная со второй половины XX века представление о значении теории и её влияние на развитие математики заметно снизились за счёт осознания возможности получения достаточно общих результатов во многих областях математики и без явного использования её аппарата, в частности, с использованием теоретико-категорного инструментария (средствами которого в теории топосов обобщены практически все варианты теории множеств). Тем не менее нотация теории множеств стала общепринятой во всех разделах математики вне зависимости от использования теоретико-множественного подхода. На идейной основе теории множеств в конце XX века создано несколько обобщений, в том числе теория нечётких множеств, теория мультимножеств (используемые в основном в приложениях), теория полумножеств (развиваемая в основном чешскими математиками).

Ключевые понятия теории: множество (совокупность объектов произвольной природы), отношение принадлежности элементов множествам, подмножество, операции над множествами, отображение множеств, взаимно-однозначное соответствие, мощность (конечная, счётная, несчётная), трансфинитная индукция.

https://ru.wikipedia.org/wiki/Теория множеств

Was ist МНОЖЕСТВ ТЕОРИЯ - Definition